Чему равен тангенс 30° градусов - tg(30°)?

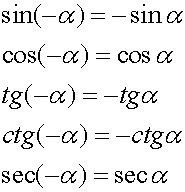
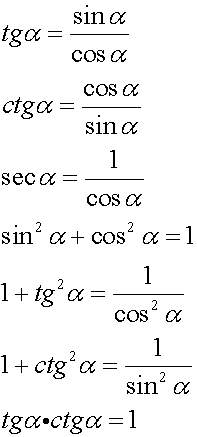
Математика – наука, которая использует часто обозначение tg, тангенс угла. Это значение легко получить если знаешь синус и косинус, так как тангенсом угла является отношение противолежащего катета к прилежащему, tg(α) = sin(α)/cos(α). Используя радиальную меру угла можем получить следующие значение: tg (30°) = (π/6).

Тригонометрия изучает различные функции и для решения задач удобно пользоваться таблицей тригонометрических тождеств. Она позволяет быстрее преобразовать функцию.

Бывают случаи, когда нужно избавиться от отрицательного значения меры угла. По этому, пользуются ещё одной таблицей по тригонометрическим тождествам. Главный их принцип – чётность и нечётность этих функций. То есть можем сделать вывод, что tg(-30°)= - tg(30°)= -(√3)/3

Как найти значение тангенса при α=30°?

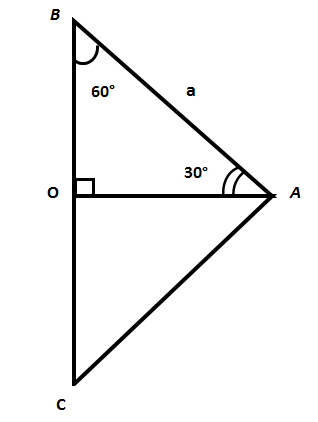
Допустим, нам дан треугольник АВС, который является равностороннем, имеет стороны а. Так в таком треугольники все углы равны, то ∠В=60°.

Из точки А на BC опустим новую сторону треугольника AO, которая одновременно является биссектрисой, медианой, высотой. ∠ВАО = 180 - 90 - 60 = 30°

Гипотенуза в данном случаи равна значению а. Сторона OB равна a/2 , учитывая, что AO является медианой в треугольнике ABC. Нужно найти катет AO. Воспользовавшись теоремой пифагора, получаем:

• АВ2=АО2+ОВ2;
• АО2=АВ2-ОВ2
• АО2=a2- (а/2)2
• АО2=3a2/4
• AO=√( 3a2/4 ) =a√3/2
  • AB = a,
  • OB = a/2,
  • AO = a√3/2 и tg 30°= OB / AO

Так как мы имеем дело с равностороннем треугольником, то BO соответствует половине стороны AB.

В результате имеем: tg(30°) = а/2 :

а√3/2=1/(√3) = (√3)/3. Тангенс тридцати градусов соответствует корню из трёх

делённому на три.