Точное значение синуса 45 градусов. Формула и расчет.
Чему равен синус 45 градусов? Формула и расчет


Способы решения геометрических задач, используя функции треугольников - это наука тригонометрия (дословно переводится, как «измерение треугольников»). Хотя еще со времен Древней Греции ученые использовали вычисленные функции для решения астрономических, архитектурных и геодезических вычислений, но только в конце шестнадцатого века немецкий математик Бартоломеус Питискус ввел этот термин для отдельного раздела математики, посвященного изучению тригонометрических функций и их приложений.
Синус 45° градусов равен √2/2
Докажем это. Чтобы определить, чему равен синус 45 градусов, необходимо построить прямоугольный треугольник АВС, примем значение угла В равным 45 градусам. Зная теорему о свойствах прямоугольного треугольника, возможно вычислить значение остальных углов. Так как треугольник является прямоугольным, следовательно угол С будет равен 90 градусам, угол В изначально равен 45 градусам, а сумма всех углов прямоугольного треугольника составляет 180 градусов.
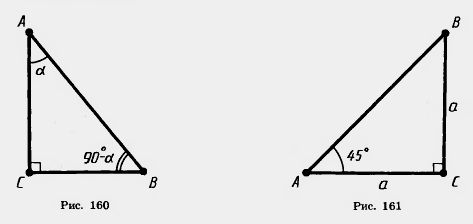
∠А + ∠В + ∠С = 180° , теперь можно вычислить значение угла А
∠А = 180° -∠С - ∠В = 180° - 90° - 45° = 45°
Теперь мы знаем, что два угла у нас равны между собой, следовательно треугольник у нас равнобедренный, значит можно использовать такое свойство равнобедренного треугольника, как равность катетов. Применяем для решения задачи теорему Пифагора
АВ2=АС2+ВС2
Заменяем стороны АС и ВС на переменную a (мы помним, что стороны у нас равны друг другу!), следовательно:
АВ2 = а2 + а2 = 2а2,
Тогда АВ=а√2.
Синус это отношение противолежащего катета к гипотенузе, где ВС – катет, АВ – гипотенуза.
sin α = BC / AB
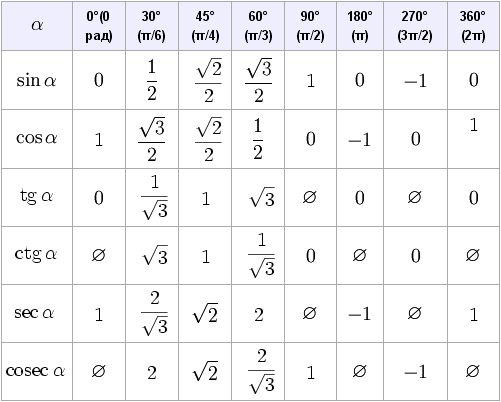
Можете также заодно узнать значение sin(135°) или синус 360° градусов.

Для меня всегда было сложной дилеммой - запомнить таблицу синусов и косинусов наизусть. Проще сделать шпаргалку в виде таблицы и применять ее на занятии по алгебре. Именно так и поступала - достаешь из учебника, подставляешь значения и продолжаешь рассчитывать уравнения.
Есть несколько вариантов расчета:
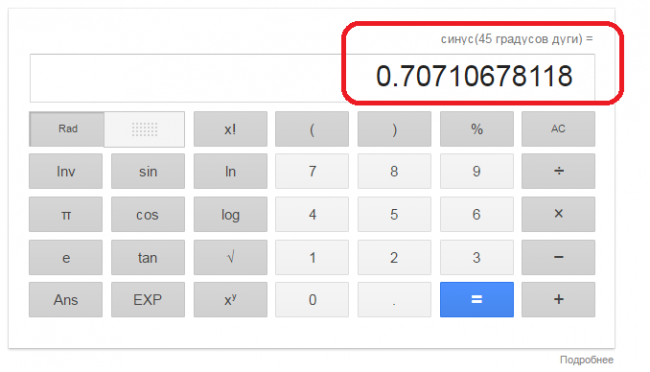
1. первый - это посредством инженерного калькулятора, который позволяет с точностью до одиннадцатых знаков выдать результат после запятой. Корректный ответ на нем будет - 0,70710678118.
2. второй - использовать приведённую ниже таблицу. Достаточно свести данные и получится, что sin 45 градусов равен корень из двух поделить на два. Если рассчитать числитель, то получится не число меньшее двойки в знаменателе. А это значит, что целое мы не получим. Так и есть, в итоге после деления выходит округленное до сотых долей число - 0,71 (при необходимости можно указать - единицу, но это будет не совсем правильно).
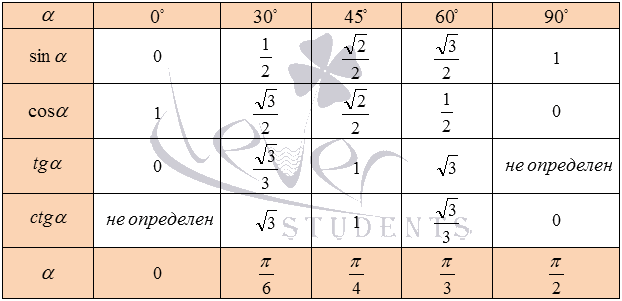
Если посмотреть, то есть два значения, которые никогда не определяются. Например, тангенс 90 градусов - не определен и тот же катангенс 0 градусов - аналогичная ситуация. Поэтому с этим примером, нам еще повезло - у него есть решение и можно довести алгебраический расчет до конца.
Что стоит прочесть, для расширения своих знаний: