Чему равен косинус 30° градусов - cos(30°)?

Достаточно вспомнить определение косинуса:

"Косинус острого угла в прямоугольном треугольнике — это отношение прилежащего катета к гипотенузе."

Наглядно это выглядит так (сторону "а" делим на строну "с", так как "а" - это катет, а "с" - это гипотенуза):

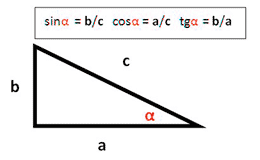
Какое значение косинуса 30 градусов?

1. Точное значение косинуса 30 градусов (используется в реальных, нешкольных задачах) = 0.15425144988.
2. В школьных задачах часто используют не точное значение косинуса 30 градусов, а не до конца посчитанное уравнение, чтобы школьники могли получить не страшный ответ из множества цифр, а точный. Итак, вот табличное значение косинуса:

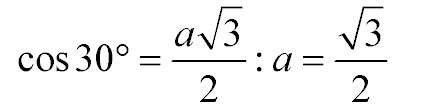
Почему так вышло? А потому что угол в 30 градусов имеет равносторонний треугольник. Потому для многих косинусов, синусов, тангенсов и котангенсов можно определить подобное значение, удобное для использования в школьных задачках.

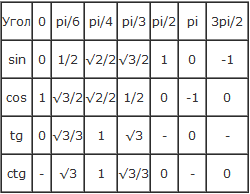
Полная таблица косинусов, синусов, тангенсов и котангенсов с указанием градусов в переводе в величину Pi:

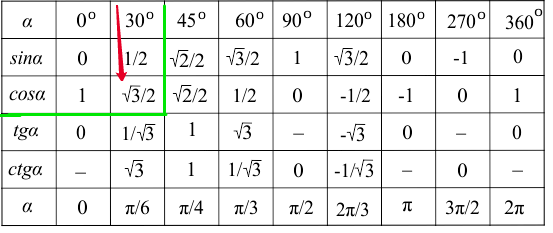
Кому интересно, можете посмотреть похожие вопросы о косинусах, чтобы полностью разобраться в теме:

• "Какой косинус 15 градусов?"
• "Какой косинус 135 градусов?"

Также советую изучить статью о тригонометрических функциях из Википедии, ведь косинус - это тоже функция.

Пусть c - гипотенуза, a - катет, прилегающий к углу 30°, b - второй катет. Искомый косинус равен отношению прилегающего катета к гипотенузе (это одно из определений, см. рис.):

Cos(30°) = a/c (1)

По теореме Пифагора: а² + b² = c² (2)

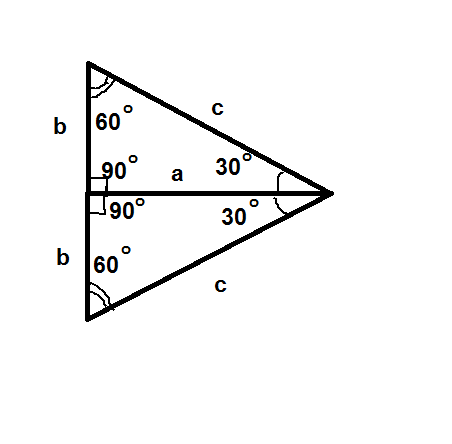
Если отразить треугольник относительно катета а, то у удвоенного треугольника все углы будут по 60°, то есть он будет равносторонним (см рис.). Следовательно,

c = 2b. (3)

Из уравнения (3) можно выразить катет b = c/2 и подставить его в уравнение (2). В итоге получится a² + c²/4 = c² или a² = 3/4c², откуда a = (√3/2)c. С учетом уравнения (1) получаем окончательно:

Cos(30°) = √3/2 или приблизительно 0,866.

Это одно из немногих значений тригонометрических функций, которое легко запомнить.

Определение

Отношение прилежащего катета к гипотенузе является косинусом угла.

Тригонометрия изучает разные формулы, их закономерности и для упрощения обозначений используется «cos». Это значение легко найти в прямоугольном треугольнике, зная стороны фигуры или углы.

сos (30°) = cos (π/6), в расчётах используют другую формулу: сos (30°) = (√3)/2 = 0,866.

Как получить косинус 30° градусов?

Математика – точная наука, но сos (30°) считается одним из самых простых значений для запоминания.

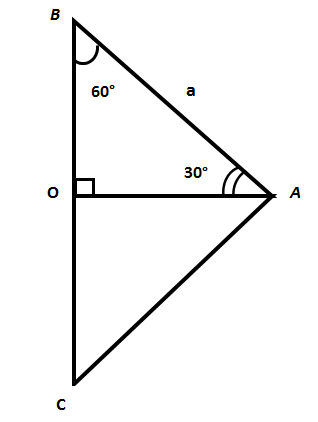
К примеру, нужно найти косинус тридцати градусов в равностороннем треугольнике с одинаковыми сторонами. Все углы равны шестьдесят градусов. После проведения медианы на сторону ВС, которая является биссектрисой, получаем прямоугольный треугольник. В нём, очевидно, есть два угла по 60, 90°. Сумма углов треугольника равна 180°, в данном случае легко можно получить третий угол, он равен разнице 180° и суммы оставшихся углов, ∠ВАО = 30°. Косинус равен отношению стороны ОА к АВ.