Почему нельзя делить на 0? Можно это логически объяснить?

Логика рассуждений при делении на ноль

Известно, что в арифметике, а сейчас говорят - в математике, - существует только два основных действия, а все остальные - это производные от них. Из школьной программы мы знаем следующие правила.

Но, действительно, давайте порассуждаем логически, почему на 0 нельзя делить. Проще говоря, такие операции не должны давать правильного результата. Известное правило из математики, что правильный результат при делении можно проверить умножением.

Для начала возьмем пример 100 : 0. При проверке умножением получаем вот такое уравнение.

0 х Х = 100

И это говорит, что при любом Х мы получим не 100, а 0.

Так что В примере на деление нет конкретного значения числа Х или ответа на пример с делением на 0.

Так что с нулем возможны следующие операции (повторение и пояснение информации представленной на рисунке).

• сложение.
• вычитание.
• умножение.

Возможно, вам будет интересно узнать:

• Можно ли решить этот пример?Х + Х + Х = 30 Вместо Х использовать можно числа
• Задача 22. Эврика: какую фразу сказал кладоискатель старцу?

Делить на ноль можно

В математике можно разделить на ноль. Однако в классической алгебре операция деления на ноль не определена в связи с возникающими трудностями. Давайте порассуждаем, почему математики для упрощения сказали, что на ноль делить нельзя.

В первую очередь допустим, что на ноль делить можно. То есть, если число разделить на ноль, то получится какое-то конкретно число. Например, 1/0=X. Теперь наша задача найти x, решить уравнение. Здесь поможет в математике понятие обратного числа.

Обратное число - это такое число, которое при умножении на данное число возвращает единицу. То есть для 1 обратным числом будет 1/1, для 2 будет обратным числом 1/2 и так далее. Определение работает и в обратную сторону, то есть для 1/2 обратным будет 2

Обратные числа определённым образом располагаются на числовой прямой: чем дальше число находится от 1, тем ближе к нулю ему обратное. Сравните, 100 и 1/100 1000 и 1/1000. Чем больше число, тем ближе к нулю ему обратное. При достаточно больших значения мы получаем число, которое будет мало отлично от нуля, но все-таки не ноль. И наоборот, чем ближе число к нулю, тем дальше находится к нему обратное. Ниже рисунок, поясняющий пример:

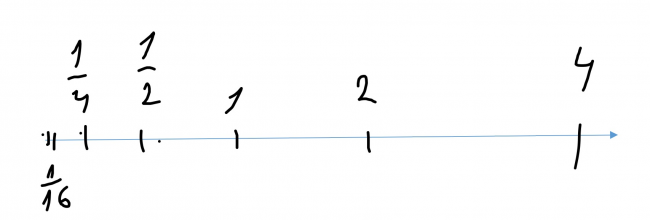
А теперь самое важное. Возьмём число 0 и попробуем отыскать к нему обратное. Это наше число x. 0 меньше любого положительного числа, а значит, обратное к нему должно быть больше любого положительного числа. Это число должно быть правой границей положительных чисел, которое положительным числом не является и за которым нет положительных чисел. А нам известно, что множество положительных чисел бесконечно. Мы получили противоречие.

Но тут есть ещё момент. Ведь же можно сказать, что 1/0=∞. Действительно, какое бы большое положительное число мы бы не взяли, бесконечность всегда будет больше этого числа. То есть ∞ и можно считать границей. Но в классической алгебре это не так. И вот почему: если начинать отчёт с нуля, то до единицы мы доберёмся за один шаг, до 2 доберёмся за 2 шага, до 100 за сто шагов. Вопрос: за сколько шагов мы доберёмся до числа ∞? Ответ: за бесконечное число шагов. Это означает, что мы никогда до него не доберёмся, так как на каком бы шагу мы не были всегда будет существовать следующий шаг, мы не доберёмся за конечное число шагов. ∞ - это не граница и вовсе не число, так как она является недостижимым значением. Таким образом, при выполнении операции деления на ноль мы как будто выпадаем из области чисел. Потому математики взяли и сказали, что делить на ноль нельзя.

Но! Следует иметь в виду, что такой раздел математики как теория функций комплексного переменного позволяет делить на ноль. За счёт именно того, что в расширенной комплексной плоскости (аналог числовой прямой для действительных чисел) бесконечность считается не недостижимым значением, а конкретной конечной (граничной) числовой точкой. Там это приводит к удивительным, но логичным фактам.

Почитайте также:

• Как основательно доказать, что 1км=1000000мм?